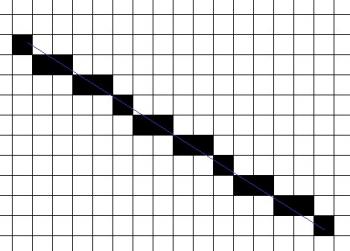
Rasterizace objetů #1: Digital Differential Analyzer
Rasteriace je proces, při kterém převádíme základní grafické objekty do systému posloupnosti obrazových bodů. Toto je důležité při práci s různými výstupními zařízeními, které nejsou schopny zobrazit přesně daný objekt, ale při svém zobrazení používají rastr.
Při rasterizaci se snažíme co nejvěrněji převést obraz do podoby rastru, a to tak, aby vznikala co nejmenší chyba (pixelizace).
Pixelizaci je možné ovlivnit použitou metodou, v případě že jí nejde zabránit, se používá například antialiasing pro její částečné odstranění.
V tomto, prvním článku, se zaměříme na rasterizaci úsečky, konkrétně na DDA Algoritmus (Digital Differential Analyzer)
Úsečka je základním grafickým prvkem, se kterým se setkáváme všude a při téměř všech operacích. Ovšem ani úsečka není v rastru dána jednoznačně a při jejím vykreslování se musíme neustále rozhodovat, kterými body (pixely) bude úsečka procházet a které z těchto, nebo okolních, bodů se vykreslí.
Všechny algoritmy, kterých existuje celá řada, vycházejí ze základní rovnice přímky:
|
1 |
<em>y = m * x + b </em> |
Úsečka je většinou zadána dvěma body, koncovými body:
|
1 2 3 |
[x<sub>1</sub>, y<sub>1</sub>] <br /> a <br /> [x<sub>2</sub>, y<sub>2</sub>] |
nebo souřadnicí jednoho bodu a vektorem:
|
1 2 3 |
[x<sub>1</sub>, y<sub>1</sub>] a ( Δx, Δy ) = (x<sub>2</sub> – x<sub>1</sub>, y<sub>2</sub> – y<sub>1</sub>) |
Dále může být zadání úsečky doplněno o různé atributy, upřesňující její zobrazení, jako barva, tloušťka a podobně.
Pro většinu algiritmů je důležitý výpočet směrnice takové úsečky:
|
1 |
m = Δy/Δx |
a posunutí úsčky:
|
1 |
b = ((x<sub>2</sub>*y<sub>1</sub>) – (x<sub>1</sub>*y<sub>2</sub>))/(x<sub>2</sub>-x<sub>1</sub>) |
DDA algoritmus (Digital Differential Analyzer)
DDA algoritmus je jednoduchý přírustkový algoritmus, který je založen na postupném přičítání přírustku k hodnotám obou os, vycházejících z jednoho bodu a jdoucí k druhému bodu, kterými je úsečka zadána.
Algoritmus jde rozdělit na několik situací, které mohou nastat. První v nich je, kdy je úsečka rovnoběžná s některou z obou os x nebo y. V takovémto případě není potřeba jednotlivé body dopočítávat, protože je samozřejmě jasné, kterými body bude úsečka procházet a které body se v tomto případě vykreslí.
Pokud je úsečka rovnoběžná s osou x, budou všechny hodnoty na ose x stejné a hodnoty na ose y se budou postupně zvyšovat o přírustek 1, v opačném případě, kdy bude úsečka rovnoběžná
s osou y, budou všechny hodnoty na ose y stejné a hodnoty na ose x se budou postupně zvyšovat o přírustek 1.
V takovém případě se budou vykreslovat jednotlivé pixely sousedící a nebude se měnit některá z jejich souřadnic.
Další dvě možnosti, kdy úsečka není rovnoběžná ani s jednou z obou os, rozdělujeme podle směrnice m.
Pokud je hodnota směrnice m < 1, budeme počítat přírustek na ose y podle vzorce:
|
1 |
y<sub>i+1</sub> = y<sub>i</sub> + m |
a hodnoty na ose se budou postupně zvyšovat o 1.
Druhý případ nastane, pokud je směrnice m > 1. V tomto případě budeme dopočítávat přírustek na ose x a hodnoty na ose y se budou postupně zvyšovat o 1:
|
1 |
x<sub>i+1</sub> = x<sub>i</sub> + 1/m |
Samozřejmě, že podle obou vzorců nebudou vycházet celá čísla, ale ve většině případů bude hodnota desetinné číslo. Hodnoty se zaokrouhlují na celá čísla podle pravidel matematiky, abychom dostali souřadnice pixelů pro vykreslení.
V hodnotě směrnice může nastat ještě jeden případ, kdy bude m = 1. V takovémto případě je možno počítat hodnoty přírustku oběma případy, protože přírustek bude roven hodnotě 1 na obou osách.
Celý princip výpočtu souřadnic je jednoduše pochopitelný na následující funkci, která je napsána tak, jak algoritmus funguje.
Funkce obsahuje 4 vstupní parametry – souřadnice dvou bodů, určující úsečku. Dle těchto bodů funkce vypisuje souřadnice nutné pro rasterizaci.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
void DDALine(int x1, int y1, int x2, int y2){ //zjistime, nejedna li se o primku if( x1 == x2 ){ //vodorovna primka: x-ova souradnice je neustale stejna. for( int i = y1; i<=y2; i++){ System.out.println(x1+" "+i); } } else if( y1 == y2 ){ //svisla primka: y-ova souradnice je neustale stejna for( int i = x1; i<=x2; i++){ System.out.println(i+" "+y1); } } //sikma usecka else{ //smernice usecky double m = (((double)(y2-y1)/(double)(x2-x1))); //pokud je smernice mensi nez jedna if( Math.abs(m) < 1 ){ //pokud je x1 vetsi nez x2, prehodime body if (x1 > x2){ int p1 = x1;int p2 = y1; x1 = x2;y1 = y2; x2 = p1;y2 = p2; } //pocatecni hodnota y double yi = y1; for (int i = x1; i <= x2; i++){ System.out.println(i+" "+Math.round(yi)); //dopocitavame y yi = ((double)(yi+m)); } } //pokud je smernice vetsi nez jedna else{ //pokud je y1 vetsi nez y2 tak prehodime body if (y1 > y2){ int p1 = x1;int p2 = y1; x1 = x2;y1 = y2; x2 = p1;y2 = p2; } //pocatecni hodnota x double xi = x1; for (int i = y1; i <= y2; i++){ System.out.println(i+" "+Math.round(xi)); //postupne dopocitavame x; xi = ((double)(xi+1/m)); } } } } |
Pro volání funkce například:
|
1 |
DDALine(1, 1, 5, 6); |
Vrací funkce hodnoty:
|
1 2 3 4 5 6 |
1 1 2 2 3 3 4 3 5 4 6 5 |
Tyto hodnoty representují x-ové a y-ové souřadnice, ve kterých se vykreslí úsečka.
Závěrem
DDA algoritmus je jeden z nejjednodušších algoritmů pro rasterizaci úsečky. V příštím článku se zaměříme na Bresenhamův algoritmus